classe 5 funzioni geogebra MATEMATICA AppassionataMenteTEOREMA di ROLLE mtb23 Giugno 202019 Marzo 2020 Lascia un commento su TEOREMA di ROLLE
classe 5 funzioni MATEMATICA AppassionataMente materiali didatticiStudio di funzione razionale fratta mtb23 Giugno 20205 Marzo 2020 Lascia un commento su Studio di funzione razionale fratta Studio di funzione razionale fratta
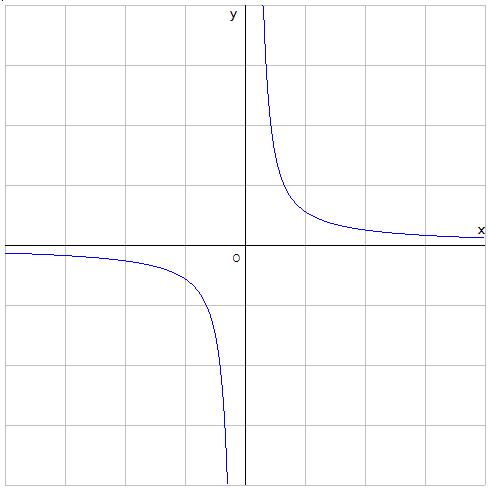
classe 5 funzioni materiali didatticiStudio di funzione RAZIONALE FRATTA mtb26 Luglio 20118 Febbraio 2011 Lascia un commento su Studio di funzione RAZIONALE FRATTA Studio di funzione RAZIONALE FRATTA (PdF) 2×2 + 1 y= ⎯⎯⎯⎯⎯⎯⎯⎯ x3 Osservare analogie e differenze con la precedente funzione 2×2 – 1 y= ⎯⎯⎯⎯⎯⎯⎯⎯ x3 Maria Teresa Bianchi © 2011
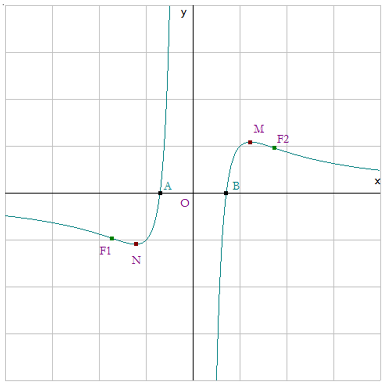
classe 5 funzioniStudio di funzione mtb20 Novembre 20127 Febbraio 2011 1 commento su Studio di funzione Studio di funzione RAZIONALE FRATTA (PdF) 2×2 – 1 y= ———– x3
classe 5 funzioniStudio di funzione RAZIONALE FRATTA mtb19 Gennaio 201119 Gennaio 2011 Lascia un commento su Studio di funzione RAZIONALE FRATTA Studio di funzione RAZIONALE FRATTA 4x y = ————- (x+4)2 Studio di funzione RAZIONALE FRATTA (PdF) ax y = ————- (x+a)2 Studio generale di funzione RAZIONALE FRATTA (PdF) Maria Teresa Bianchi ©2011
mtb
