Vai al contenuto

MaTeBi – Maria Teresa Bianchi

Cucina, Matematica … il mio web

  • CUCINARE AppassionataMente
    • 01 antipasti
    • 02 primi
    • 03 secondi
    • 04 carni
    • 05 pesce molluschi crostacei
    • 06 salse
    • 07 verdure legumi patate
    • 08 dolci e dessert
    • 09 pane e lievitati
    • 10 piatti unici
    • 11 menu
    • 12 consigli
    • 13 varie
    • 14 estemporanei
  • MATEMATICA AppassionataMente
    • PI DAY 2012
    • PI DAY 2013
    • PI DAY 2014
    • PI DAY 2015
    • PI DAY 2017
    • PI DAY 2018
    • PI DAY 2019
    • PI DAY 2020
classe 5 / funzioni / MATEMATICA AppassionataMente / materiali didattici

Studio di funzione razionale fratta

Pubblicato il: 5 Marzo 202023 Giugno 2020

Studio di funzione razionale fratta

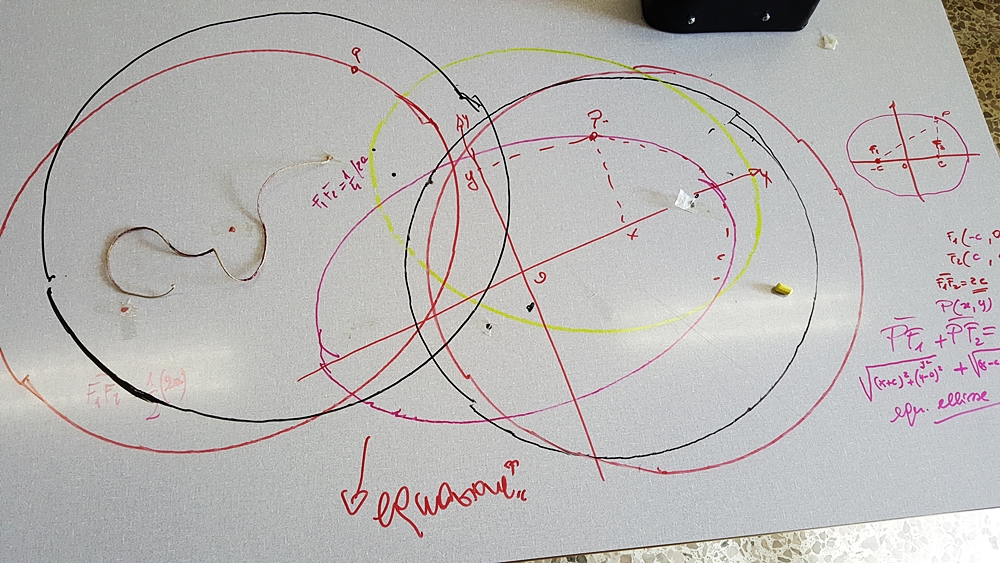
Ellisse
classe 3 / MATEMATICA AppassionataMente / materiali didattici

Ellisse

Pubblicato il: 6 Aprile 20186 Aprile 2018

E le ellissi disegnate sulla cattedra dagli alunni con spago, scotch e pennarelli fanno capire molto più di una lunga spiegazione!

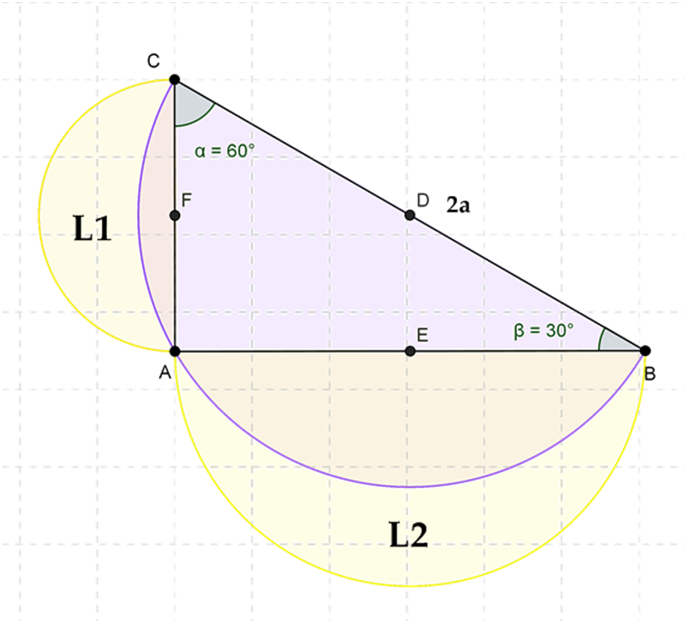
Lunule di Ippocrate
geogebra / MATEMATICA AppassionataMente / materiali didattici / storia della matematica

Lunule di Ippocrate

Pubblicato il: 12 Giugno 201414 Giugno 2014

Da un test universitario … alcune riflessioni sulle LUNULE di IPPOCRATE Maria Teresa Bianchi, febbraio 2014 Dato un triangolo rettangolo di ipotenusa 2a e un angolo di 60° […]

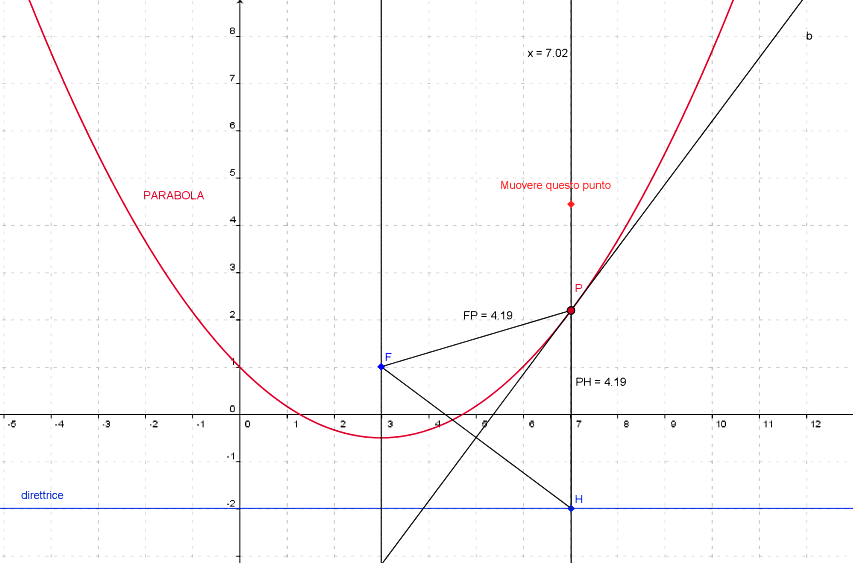
Costruzione di una parabola
classe 3 / geogebra / materiali didattici

Costruzione di una parabola

Pubblicato il: 19 Febbraio 201126 Luglio 2011

Vai alla costruzione con GEOGEBRA (dati fuoco e direttrice fissi) Vai alla costruzione con GEOGEBRA (data direttrice fissa e fuoco variabile) Muovere il fuoco F e lasciare fissa […]

Studio di funzione RAZIONALE FRATTA
classe 5 / funzioni / materiali didattici

Studio di funzione RAZIONALE FRATTA

Pubblicato il: 8 Febbraio 201126 Luglio 2011

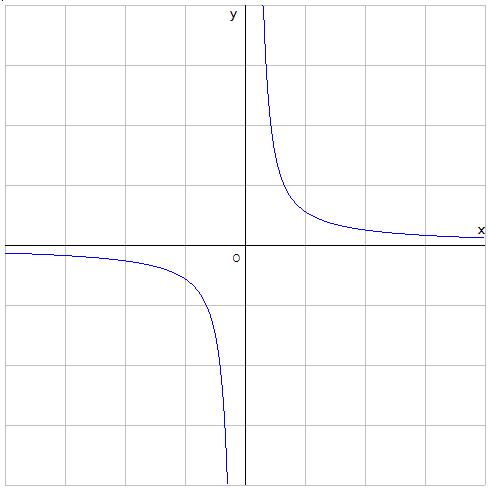
Studio di funzione RAZIONALE FRATTA (PdF)        2×2 + 1 y= ⎯⎯⎯⎯⎯⎯⎯⎯        x3 Osservare analogie e differenze con la precedente funzione         2×2 – 1 y= ⎯⎯⎯⎯⎯⎯⎯⎯        x3 Maria […]

Paginazione degli articoli

Pagina 1 Pagina 2 … Pagina 10 Pagina successiva

ciao

Benvenuti qui!
Cucina, matematica, conversazioni ... tutto il mio web.
Grazie ai numerosi visitatori anche se silenziosi ...
Maria Teresa

I miei blog 
Cucinare... AppassionataMente
Matematica ... AppassionataMente
sono "nati"  nel 2003 in altre piattaforme.

Qui anche il blog di biblos (Sergio): Il piacere di leggere

Archivi

Dicembre 2024
L M M G V S D
 1
2345678
9101112131415
16171819202122
23242526272829
3031  
« Nov    

da Sergio … per me

Chissà se in qualche libro di cucina
C’è la ricetta della felicità?
Chissà in quali ingredienti si declina
Se prepararla sia semplice, in realtà?
Come chi del viaggiare ama il viaggio
Del cucinare tu ami gli ingredienti
Il farli stare insieme, amalgamarli
Immaginare che si sentano contenti
Il risultato? Conta, ma di certo
Non come quella gran soddisfazione
Di trasformare un ordine imperfetto
Nella Parigi dopo la Rivoluzione

da Sergio ... per me

Articoli recenti

  • Terza Domenica d’Avvento 2024
  • Vitello tonnato (ricetta di Daniele Persegani)
  • Seconda domenica d’ Avvento 2024
  • Spezzatino di cinghiale
  • Prima Domenica d’Avvento 2024

Meta

  • Accedi
  • Feed dei contenuti
  • Feed dei commenti
  • WordPress.org
DISCLAIMER

Le ricette pubblicate fanno parte del mio bagaglio: le ricette della mia mamma, scambi con amiche, letture di riviste e libri, ricette della tradizione, rivisitazioni personali, piatti assaggiati in qualche ristorante e provati a casa. Potrebbe accadere che alcune ricette siano state pubblicate in riviste, libri o in rete e io non ne conosca la fonte. Alcune immagini presenti in questo blog sono state reperite in internet. Chi ritenesse, per qualsiasi motivo, danneggiati i diritti d'autore può contattarmi per chiederne la rimozione. Grazie.

arancia auguri baccalà Bimby biscotti blog carciofi carne cipolla dolci estate Festa dei ceri foto funghi Gubbio legumi MATEMATICA AppassionataMente melanzane Natale pane panini Pasqua pasta pasta fresca patate pentola a pressione peperoni pesce poesia pollo polpette pomodori ricette regionali ricette tradizionali umbre ricordi ricotta riso risotto ristoranti torta torta al formaggio torta di Pasqua torta salata verdure zucchine

  • Benedizione del cibo
  • La storia della Festa dei Ceri
  • Festa dei ceri 2006
  • Cestini di stoffa

Tema Cube Blog di Kantipur Themes
Utilizziamo i cookie per essere sicuri che tu possa avere la migliore esperienza sul nostro sito. Se continui ad utilizzare questo sito noi assumiamo che tu ne sia felice.OkNo