classe 2 Archivi - MaTeBi - Maria Teresa Bianchi

FOTO PI DAY 2014

mtb27 Maggio 201616 Marzo 2014Lascia un commento

Liceo Classico “G. Mazzatinti” – Class 3 A LC insieme a 1 ALC-2 ALC Maria Teresa Bianchi VAI ALLA PAGINA per vedere video e foto: PI DAY 2014 VAI ALLA PAGINA per vedere video e …

classe 2

La storia delle “patatine”

mtb22 Settembre 201218 Settembre 2012Lascia un commento

Questo è un blog di cucina, ma anche di matematica e le patatine sono un pretesto per fare un po’ di matematica. Quest’estate mentre eravamo a cena in un ristorante della città, accanto a noi …

classe 2 geogebra materiali didattici

Teorema di Pitagora di Liu Hui

mtb7 Febbraio 20114 Febbraio 20112 commenti

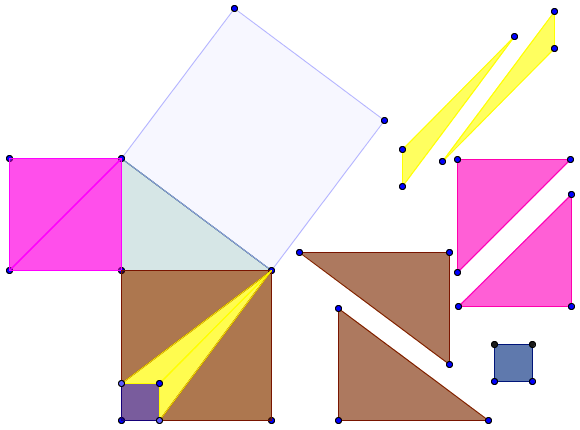
Liu Hui e il Teorema di Pitagora Vai alla costruzione di Liu Hui eseguita con Geogebra

classe 2 materiali didattici

Generalizzare da un semplice problema

mtb31 Marzo 202016 Gennaio 2011Lascia un commento

Dato un rettangolo di base b e altezza h, se si incrementano le due dimensioni di una stessa quantità, quale è la differenza dei perimetri dei due rettangoli? E quella delle aree? Generalizzare da un …

classe 2 materiali didattici

Problema: modello matematico e riflessioni in classe

mtb26 Luglio 20118 Novembre 20102 commenti

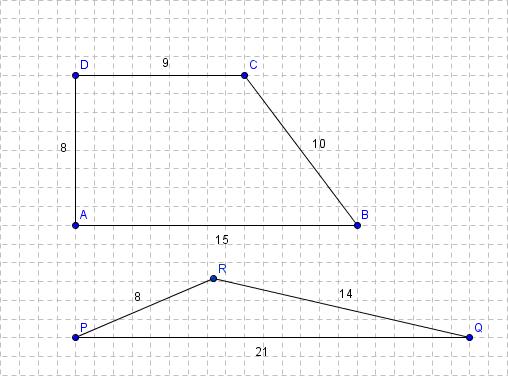
Partendo da un problema semplice si possono far riflettere gli alunni sul modello matematico, sui vincoli, sull’avere soluzioni o meno, sulla geometria applicata a situazioni reali e molto di più. Il testo del problema: Date due …

classe 2 classe 3 classe 4 classe 5 MATEMATICA AppassionataMente materiali didattici

Materiali didattici: un breve riepilogo

mtb4 Luglio 200830 Maggio 20075 commenti

Downloads: Suggestioni numeriche 815.00 Kb Scheda di riepilogo: radicali 182.80 Kb Espressioni letterali e dominio in R 100.13 Kb Studio di ax+by+c=0 206.02 Kb Scheda di riepilogo: ax+by+c=0 182.70 Kb Studio di y = a x² + b x + …

articoli vari poesia libri classe 2 MATEMATICA AppassionataMente

XVIII CERTAMEN PELORITANUM

mtb13 Luglio 200811 Maggio 200623 commenti

In bocca al lupo ai miei alunni che parteciperanno al XVIII CERTAMEN PELORITANUM gara nazionale di Latino aperta agli alunni di tutti i Licei. Il Certamen avrà luogo Sabato 13 MAGGIO 2006 a MESSINA, al LICEO …

classe 2 dal blog precedente MATEMATICA AppassionataMente materiali didattici

Il blog della classe 2ALC 2003-2004

mtb25 Luglio 201124 Luglio 20041 commento

Il film “TROY” Sabato 29 Maggio 2004 ore 07:08:19 Troy Nazione: Usa Anno: 2004 Genere: Azione/Guerra/Drammatico Durata: 163′ Regia: Wolfgang Petersen Cast: Brad Pitt, Eric Bana, Orlando Bloom, Diane Kruger, Sean Bean, Brian Cox, Peter …

avvisi classe 2 MATEMATICA AppassionataMente

Classe 2ALC

mtb14 Gennaio 200812 Giugno 20042 commenti

Venerdi 5 Dicembre 2003 ore 14:37:53 E’ in preparazione il blog per la classe 2ALC… abbiate un po’ di pazienza mtb